Title: Rubio de Francia Extrapolation
Abstract: The classical Rubio de Francia Extrapolation establishes that if an operator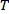 
is bounded on 
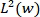for all 
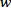in the Muckenhoupt class of weights 
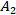, then 
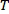is also bounded on all 
for all 
and all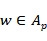 
. In the last forty years, Rubio de Francia’s result has been extended and complemented in several different ways. In particular, one can also derive the boundedness of 
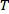on many different function spaces. All these results show, in hindsight, that what is needed to extrapolate to a given weighted function space, requires assumptions on the weight guaranteeing that the Hardy-Littlewood maximal function is bounded. During this mini-course we will present a new abstract approach to extrapolation on which one can reduce matters to constructing Muckenhoupt weights so that there is some “embedding” between the functions spaces in the conclusions and the ones in the hypotheses. More precisely, in the classical Rubio de Francia Extrapolation one would need to see how to “embed” 
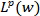, for a given 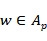, into 
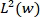for some 
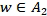, and viceversa. An important feature is that global embeddings are not needed, rather we can work function by function and the constructed weights depend very much on the functions we are dealing with.
We will consider several applications of the abstract extrapolation theory: well-posedness results for some Dirichlet problem in the upper half-space whenever the boundary data belongs to a general weighted spaces; weighted inequalities for the layer potential operators and the related commutators on uniformly rectifiable domain; and limited range extrapolation result for operators associated with the Kato conjecture.
Content:
1. Introduction
2. Calderón-Zygmund theory, Muckenhoupt weights, and functions spaces.
3. Rubio de Francia extrapolation in Lebesgue spaces
4. Rubio de Francia extrapolation in function, modular, and tent spaces
5. Applications
5.1. The Dirichlet problem in the upper half-space
5.2. Layer potentials on uniformly rectifiable domains
5.3. Operators associated with the Kato conjecture
Resumé of the Lecturer: José María Martell is Investigador Científico at the Instituto de Ciencias Matemáticas – ICMAT (Institute for mathematical Research). His main research areas are harmonic analysis, partial differential equations, and geometric measure theory. In particular, his research has dealt with the Calderón-Zygmund theory, weighted norm inequalities, Poincaré type inequalities, wavelets, operators associated with the Kato conjecture, elliptic PDE with rough coefficient in rough domains, etc. J.M. Martell is the Vice-president for Scientific and Technical Research (VICYT) of the Spanish National Research Council (CSIC) since July 2022. He was the Director of the ICMAT from January 2020 to July 2022, and its Interim Director and the Deputy Director. Additionally, he was the Director of the CFTMAT (Centro de Física Teórica y Matemáticas) from February 2020 to July 2022.
